第5章-广度优先搜索

广度优先搜索

广度优先搜索：找到两样东西之间的最短距离，不过最短距离的含义有很多

 编写国际跳棋AI，计算最少走多少步就可获胜；

 编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如：READED改为READER需要编辑一个地方；

 根据你的人际关系网络找到关系最近的医生。

解决最短路径问题的算法被称为广度优先搜索。需要两个步骤：

1. 使用图来建立问题模型。
2. 使用广度优先搜索解决问题。

图是什么

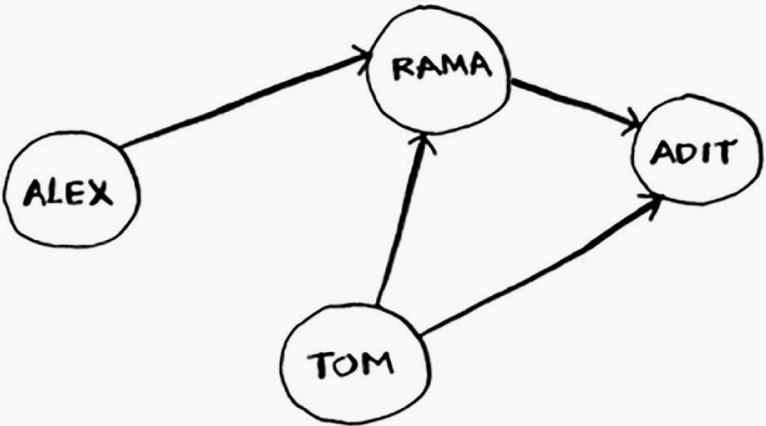
图由接地那和边组成。一个节点可能与众多节点直接相连，这些节点被称为邻居

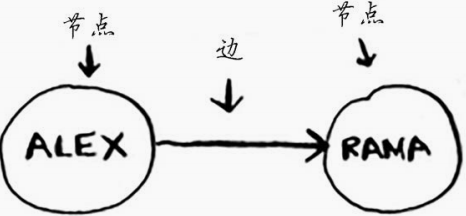
广度优先搜索

前面我们学习过二分查找。广度优先搜索时一种用图的查找算法，可以帮我我们回答两类问题：

1. 从A节点出发，能否到达B节点
2. 从A节点出发，到达B节点最短路径是什么？

查找最短路径

队列 (queue)

队列是一种先进先出（First In First Out，FIFO）的数据结构，而栈是一种后进先出（Last In First Out，LIFO）的数据结构。

实现图

首先，需要使用代码来实现图。图由多个节点组成。

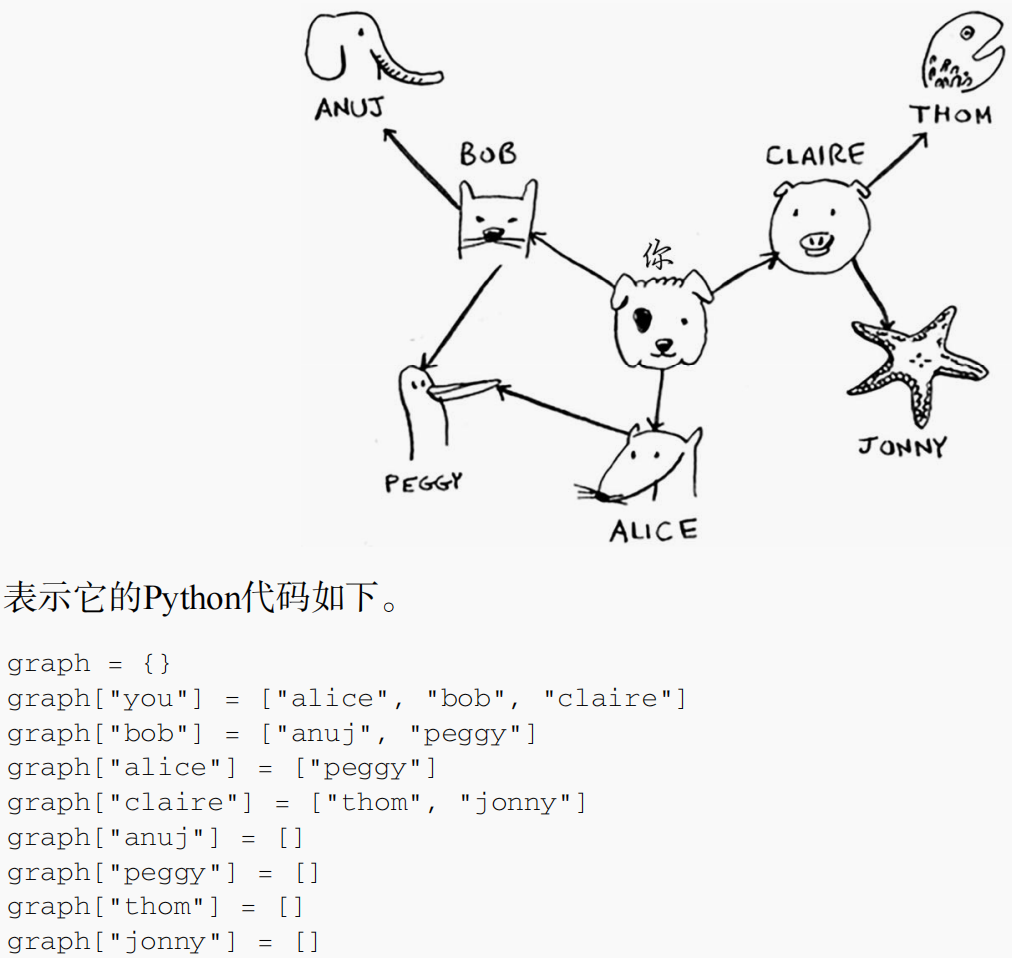
实现算法

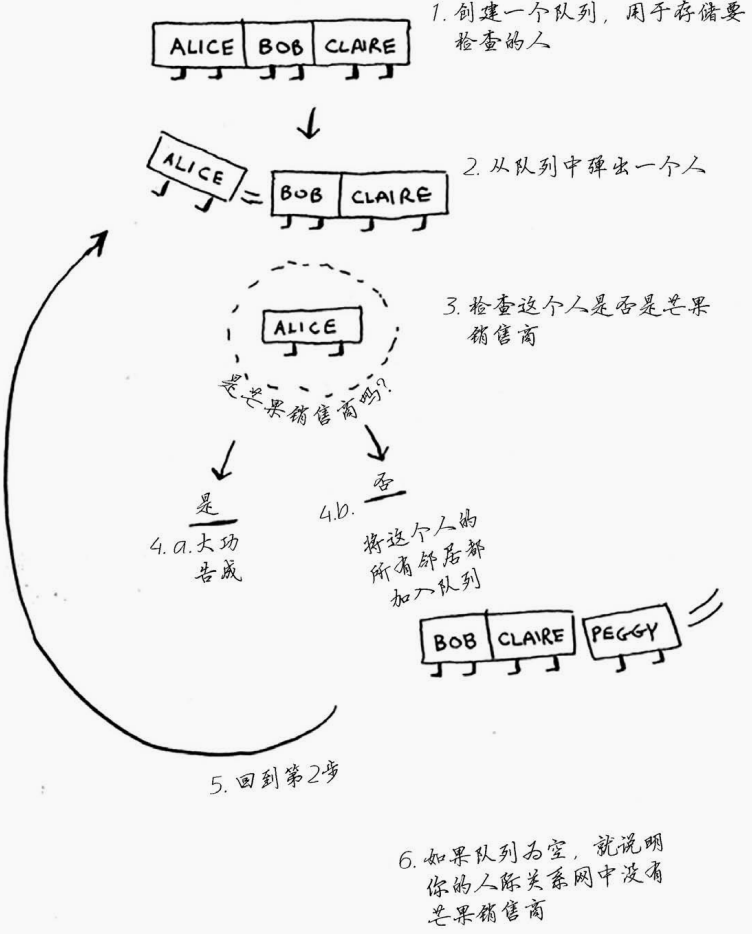
• 更新队列时，我使用术语“入队”和“出队”，但你也可能遇到术语“压入”和“弹出”。压入大致相当于入队，而弹出大致相当于出队。

检查一个人之前，要确认之前没检查过他，这很重要。为此，你可使用一个

列表来记录检查过的人。

考虑到这一点后，广度优先搜索的最终代码如下。

def search(name): 
  search_queue = deque() 
  search_queue += graph[name] 
  searched = [] 
  while search_queue: 
    person = search_queue.popleft() 
    if not person in searched:
      if person_is_seller(person): 
        print person + " is a mango seller!" 
        return True 
      else: 
        search_queue += graph[person] 
        searched.append(person)
  return False

运行时间

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。

你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。

小结

• 广度优先搜索指出是否有A到B的路径

• 如果有，广度优先搜索将找出最端路径

• 面临类似于寻找最短路径的问题时，可以尝试使用图来建立模型，再使用广度优先搜索来及解决问题。

• 有向图中的边为箭头，箭头的方向指定了关系的方向，例如，rama→adit表示rama欠adit钱。

• 无向图中的边不带箭头，其中的关系是双向的，例如，ross - rachel表示“ross与rachel约

  会，而rachel也与ross约会”。

• 队列是先进先出（FIFO）的

• 栈是后进先出（LIFO）的。

• 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列。

• 对于检查过的人，务必不要再去检查，否则可能导致无限循环。