第3章 排序

第 3 章 排序

快速排序

你要在一个列表中找到播放量最高的歌，你需要遍历一遍这个列表，找出最高的，时间复杂度就是O(n)，但是如果你想对这个列表排序，就需要找n次最小(大)的

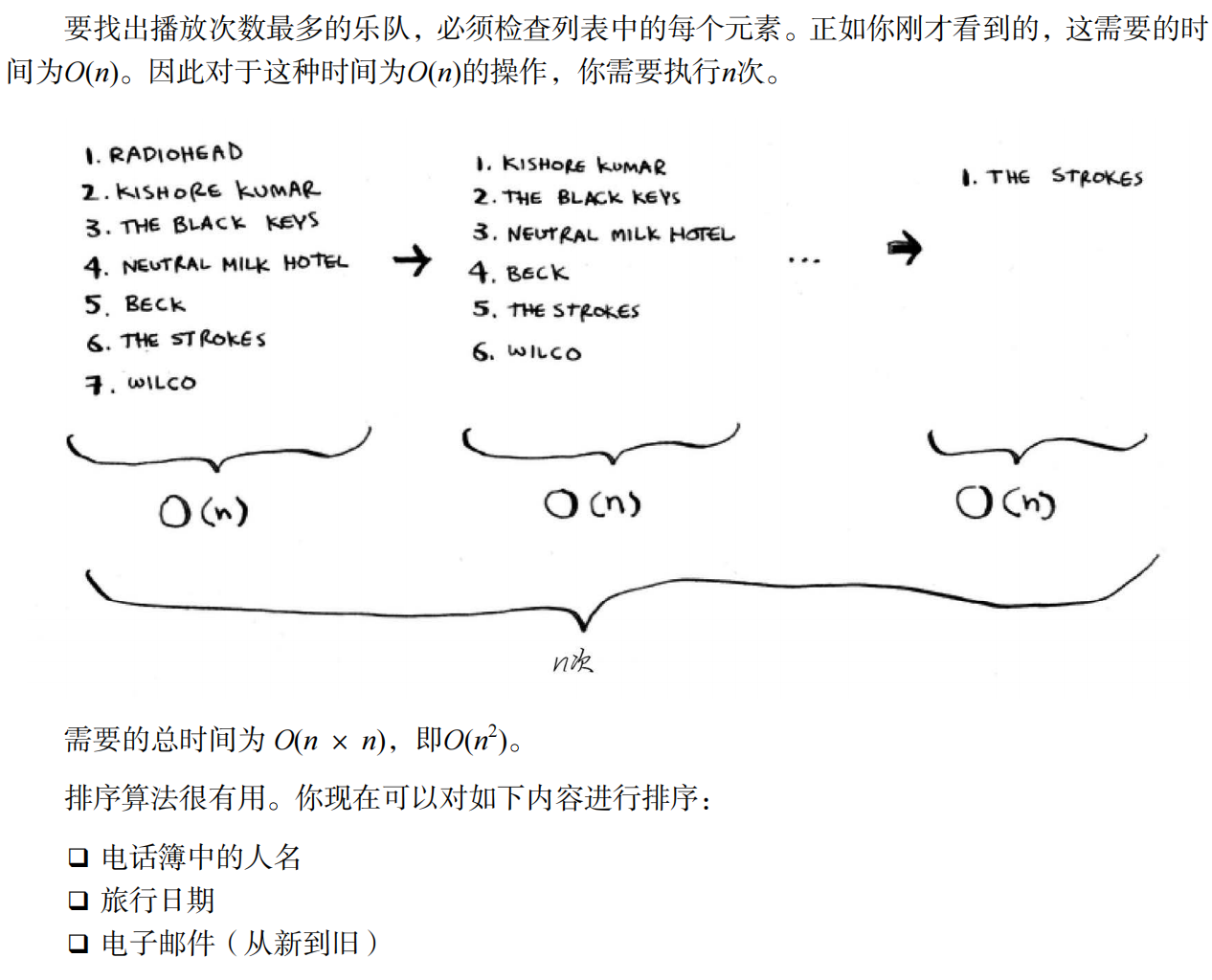
需要检查的元素数越来越少

随着排序的进行，每次需要检查的元素数在逐渐减少，最后一次需要检查的元素都只有一个。既然如此，运行时间怎么还是O(n2 )呢？，这与大O表示法中的常数相关。数依次为n  1, n – 2, …, 2和1。平均每次检查的元素数为1/2 × n，因此运行时间为O(n × 1/2 × n)。但大O表示法省略诸如1/2这样的常数，因此简单地写作O(n × n)或O(n2 )。

示例代码

先写一个找最小数的函数

def findSmallest(arr):
  smallest = arr[0]
  smallest_index = 0 
  for i in range(1, len(arr)): 
    if arr[i] < smallest: 
      smallest = arr[i] 
      smallest_index = i 
  return smallest_index

现在就可以编写排序算法了，找到一个最小的就删除掉一个。

def selectionSort(arr):
  newArr = [] 
  for i in range(len(arr)): 
    smallest = findSmallest(arr)
    newArr.append(arr.pop(smallest)) 
  return newArr

快速排序

探索分而治之（divide and conquer，D&C）一种注明的递归式问题解决方案。

分而治之

使用分而治之D&C解决问题的过程包含两个步骤：

1. 找出极限条件，这种条件必须尽可能简单。
2. 不断将问题分解（或者说缩小规模）直到符合基线条件。

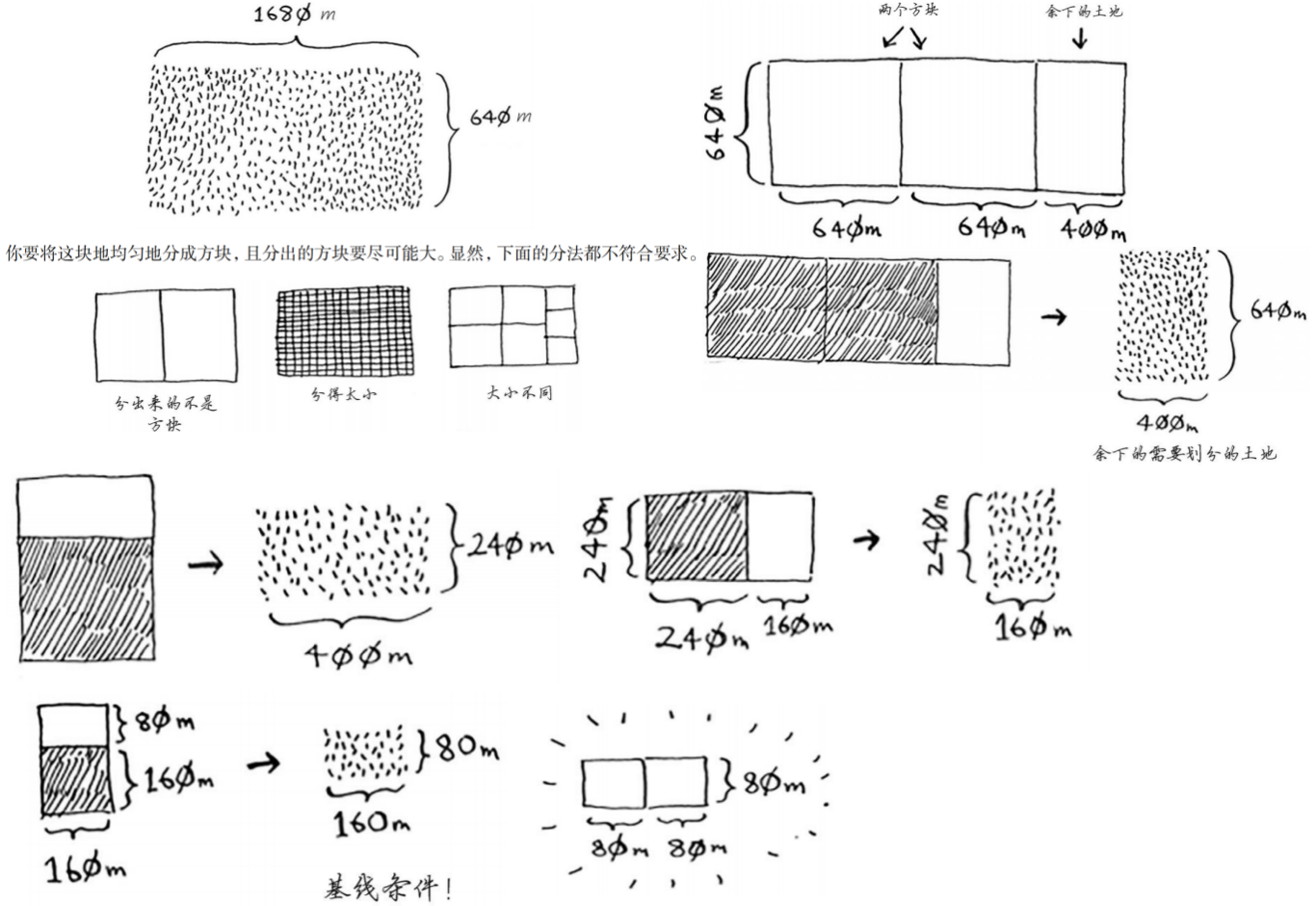
前面说“适用于这小块地的最大方块，也是适用于整块地的最大方块”，可以去了解一下 欧几里得算法

这里重申一下D&C的工作原理：

(1) 找出简单的基线条件；

(2) 确定如何缩小问题的规模，使其符合基线条件。

D&C并非可用于解决问题的算法，而是一种解决问题的思路。我们再来看一个例子。给定一个数字数组。

【2,4,6】

你需要把这些数字相加，返回结果，使用循环可以很容易完成这种任务。

但如何使用递归函数来实现呢？

第一步：找出基线条件。最简单的数组是什么样子的？不包含任何元素，只包含一个元素。这就是最简单的基线条件。

第二步：每次递归都不许离空数组更近一步，如何缩小问题的规模呢？计算列表中处理第一个数字以外的其他数字的总和，将其与第一个数字相加，再返回结果

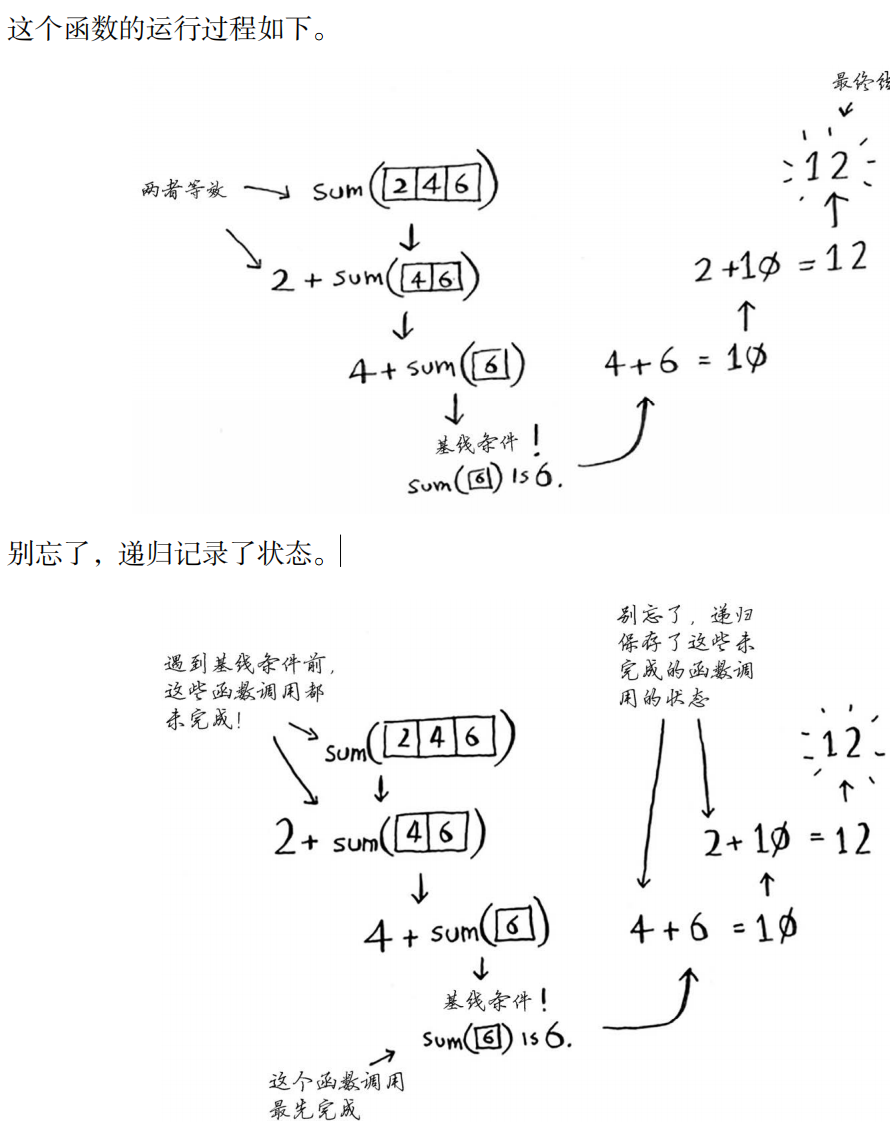
编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素

快速排序

快速排序是一种常用的排序算法，比起选择排序快很多，例如C语言标准库中的函数qsort实现的就是快速排序。快速排序也使用了D&C。

下面来使用快速排序对数组进行排序，对于一个数组莱索，最简单的数组是什么样的呢？当然是没有元素和只有一个元素的呢。

所以快速排序的基线条件也是空或者只包含一个元素，这种情况下只需要原乡返回数组就行，压根不需要排序。

我们来看看更长的数组呢，对于一个包含两个元素的数组，进行排序也是很容易的。检查第一个元素是否比第二个元素大，如果比第二个元素大，就交换他们的位置

包含三个元素呢，使用D&C，因此需要将数组分解，直到满足基线条件为止